คณิตคิดสนุก ในทฤษฎีพระเคราะห์สนธิ ตอน 3

โพสต์ 28 ส.ค.56 11:10 น. : อ่าน 25472

บทความนี้มี ตอนที่ 1 และ ตอนที่ 2 ด้วย

2. ว่าด้วย A-B และโค้งสุริยาตร์

เราอาจเคยเห็นโปรแกรมทางโหราศาสตร์บางโปรแกรม มีฟังก์ชั่นให้สามารถสร้างตารางผลต่าง (Difference) ระหว่างปัจจัย A-B ซึ่งสามารถนำมาใช้ประโยชน์ได้ดี เช่น

1) หากสมการมีคำองศาเท่ากัน ย่อมนำมาสร้างเป็นพระเคราะห์สนธิจุดอิทธิพลได้ เช่น หาก A-B=C-D นั่นย่อมหมายถึงว่า A=B+C-D นั่นเอง ตามกฎของการย้ายข้าง (ถ้าเป็น A+B=C+D ก็ทำนองเดียวกัน)

2) ผลต่างของ A-B มีความหมายในดวงจรอายุขัยประเภทโค้งสุริยาตร์ด้วย เพราะผลต่างดังกล่าวย่อมเป็นค่าโค้งที่จะทำให้ปัจจัย B จรบวกโค้งจะสัมพันธ์กับปัจจัย B เช่น หาก A-B = 35:43 องศา หมายถึงว่าเมื่อโค้งสุริยาตร์มีค่า 35:43 Bv จะเท่ากับ Ar พอดีเป๊ะ

3) และเช่นกัน A+B ซึ่งก็คือ A-(-B) ย่อมหมายถึงว่า -Bv = Ar ตามค่าองศาที่ได้นั่นเอง

 

3. ว่าด้วย Aspect Line ในภาพดวง

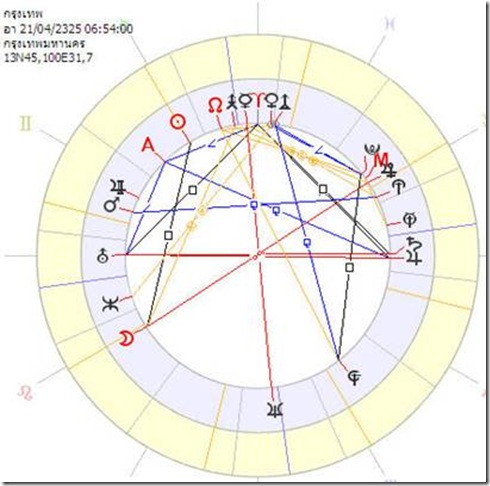
จากภาพเป็นตัวอย่างภาพดวงซึ่งแสดงให้เห็น Aspect Line ที่เราอาจพบได้ทั่วไปในโปรแกรมโหราศาสตร์สากล (ในที่นี้แสดงเฉพาะมุมประเภท Hard Aspect) นอกจากเราจะพิจารณาปัจจัยเดี่ยวที่ทำมุมถึงกันแล้ว เราอาจมองเห็นในรูปของพระเคราะห์สนธิแบบ ศูนย์รังสีและจุดอิทธิพลได้เช่นกัน

(1) กรณีที่เราเห็นเป็นภาพสามเหลี่ยมหน้าจั่ว(ตรีโกณ) เราย่อมพบว่ามันคือภาพพระเคราะห์เข้ารูปของ A=B/C นั่นเอง เช่น จากภาพ AR=JU/UR เป็นโครงสร้าง T-Sqr และ AS=AR/UR เป็นโครงสร้าง T045

(2) ปัจจัยที่ทำมุมถึงกันในมุมเดียวกัน จะเป็นพระเคราะห์สนธิในรูปแบบของจุดอิทธิพล A+B-C=D (โครงสร้างจตุโกณ) เช่นจากภาพ AS=UR และ VE=PL ในมุม 45 องศาเหมือนกัน เมื่อนำมาพิจารณาร่วมกันเราอาจจะเขียนในรูปสมการได้ว่า UR+PL-VE=AS ในมุม 0 องศา หรือ AS=JU และ MA=KR ในมุม 135 เราก็สามารถเขียนได้ว่า MA+JU-KR=AS ในมุม 0 องศา เช่นกัน (อาจต้องระวังเรื่องของระยะวังกะด้วย)

(3) จากภาพหากเรามองด้วยสายตาจะพบว่าในดวง SU มีระยะห่างกับ AS ใกล้เคียงกับ PO ห่างกับ MO เราจึงสามารถเขียนในรูปของพระเคราะห์สนธิได้ว่า SU+MO-PO=AS ในมุมกุม(0 องศา)เช่นกัน

(4) พระเคราะห์สนธิดังกล่าวย่อมมีอิทธิพลมากเป็นพิเศษเนื่องจากเป็นพระเพคราะห์สนธิแท้ (ข้อ (1)เป็นตรีโกณ ข้อ(2)(3)เป็นจตุโกณ) ซึ่งเราสามารถมองเห็นภาพประจักษ์ชัดด้วยตาเปล่าในภาพดวง

(5) ข้อน่าสังเกตที่น่าจะต้องพิจารณา กรณีที่ในดวงมีปัจจัยที่กุมกัน 2 ชุดเราก็ย่อมสามารถเขียนในเป็นพระเคราะห์สนธิในรูปของ A+B-C=D เช่นในดวงเราพบว่า VE กุม VU และ JU กุม SA เราย่อมเขียนได้ว่า VU+JU-SA=VE ในมุมกุม(0 องศา) แต่หากมองด้วยสายตาจะพบว่า VE ไม่ได้ทำมุมสำคัญใดๆกับ JU เลยเราจะมองความสัมพันธ์แบบนี้อย่างไรดีล่ะ

4. การแสดงผลของพระเคราะห์สนธิในดวงจรอายุขัย

1) ทั้งหมดที่ได้เกริ่นมาเพื่อที่จะบอกข้อสรุปว่า โครงสร้างพระเคราะห์สนธิในรูปของจุดอิทธิพลที่เราค้นพบในดวงกำเนิด จะมีช่วงเวลาแสดงผลเมื่ออายุขัยของเจ้าชะตาจรมาสอดคล้อง เช่นในข้อ(5) การแสดงผลย่อมจะเกิดขึ้นเมื่อ JUv จรมาสัมพันธ์ถึง VEr

2) นี่คือหลักเกณฑ์ที่เราจะพิจารณาปัจจัยที่จะแสดงผลในดวงจรตามอายุขัย ว่าด้วย แกนถึงแขนและแขนถึงแกนนั่นเอง (กรณีโครงสร้างตรีโกณ)

3) เราสามารถพิจารณาเงื่อนไขที่พระเคราะห์สนธิ(กรณีโครงสร้างจตุโกณ) A+B-C จะแสดงผลเมื่อ

ก) r A+B-C =v C

ข) v A+B-C =r C

ค) r A+B-C =v A/B หรือ v A/B =r C

ง) v A+B-C =r A/B หรือ r A/B =v C

4) ในการตรวจสอบดวงจรทั้งดวงโค้งสุริยยาตร์ และดวงจร Transit หากพบชุดสมการที่มีความสัมพันธ์ถึงกันหมด(อาจเรียกว่าครบวงจรก็ได้มั้ง) ให้พิจารณาเป็นพิเศษเพราะนั่นหมายถึงว่าภาพดาวนั้นกำลังแสดงผลเช่น

ก) t A+B-C=v A+B-C , v A+B-C=r C

ข) t A+B-C=v A+B-C , v A/B=r C

ค) t A+B-C=v A+B-C , r A/B=v C

ง) t A+B-C=r A+B-C , v A+B-C=r C

จ) t A+B-C=r A+B-C , v A/B=r C

ฉ) t A+B-C=r A+B-C , r A/B=v C

หากมีโครงสร้างลักษณะดังกล่าวเกิดขึ้นให้ถือว่ามีความเป็นไปได้สูงที่จะเกิดเหตุการณ์ณืเป็นไปตามความหมายของสมการนั้น ทั้งนี้จะต้องตรวจสอบด้วยว่าสมการดังกล่าวถึงจุดเจ้าชะตามากน้อยเพียงใด จะยิ่งเพิ่มน้ำหนักในการพยากรณ์จรออกไปได้ดียิ่งขึ้น

และจากประสบการณ์ A+B-C = A/B//C หรือ A/B//C = A/B//C ก็สามารถแสดงผลได้เช่นกัน

5. การแก้สมการด้วยหลักคณิตศาสตร์ ย้ายข้างไปมา

1) Av/Br=Cr จะแก้สมการได้ว่า Av=Cr+Cr-Br

2) Av/Br=Cv จะแก้สมการได้ว่า Br=Cv+Cv-Av

สมการดังกล่าวเราจะพบว่า การผสมปัจจัยข้ามวงดวงกันมิใช่ทำกันแบบลอยๆ เพราะโดยเนื้อแท้แล้วจะไม่ได้มีการผสมสมการข้ามดวงกันจริง เพียงแต่เป็นการลดรูปลงมาเพื่อเห็นภาพจากดวงได้ง่ายขึ้นเท่านั้น ในส่วนตัวของข้าพเจ้าจึงไม่ใช้สมการข้ามวงดวงกันโดยไม่มีที่มาที่ไป เพื่อพยายามจะหาสูตรดาวที่มันเข้ากับเรื่องราว

6. บางสมการใช้ไม่ได้ เพราะมันเป็นเพียงภาพลวงตา

เนื่องจากพบว่ามีพระเคราะห์สนธิบางรูปแบบที่เป็นเหมือนภาพลวงตาทางคณิตศาสตร์ หากนำมาใช้เกรงว่าจะทำให้สับสนจึงน่าจะต้องระมัดระวังบ้าง เช่น

1) A+B-C=A หรือ A+B-C=B เพราะจริงแล้วหากย้ายข้าง A มา เราจะได้ B=C นั่นเอง จึงไม่ได้มีอะไรเกี่ยวข้องกับ A เลย

2) A+B-C = -C หรือ A+B+C=C หากย้ายข้าง -C มาก็คือ A= -B หรือ A+B=AR จึงไม่มีอะไรเกี่ยวกับ C เลยเช่นกัน

7. แถมท้าย เป็นการบ้าน

มีพระเคราะห์สนธิแปลกๆแบบหนึ่งที่เราอาจพบในดวงกำเนิดคือ A+B-C=A/B//C ซึ่งบางท่านอาจมองว่าหมายถึงความครบวงจรของสมการ แต่ที่จริงหากถอดสมการแล้วสมการแบบนี้เกิดมาจาก A/B ทำมุมกับ C ในมุม Hard Aspect(จำนวนเท่าของ 45 องศา) หรือ Soft Aspect(จำนวนเท่าของ 30 องศา) ลองตรวจสอบดูเอาเองนะครับ

นี่เป็นเพียงตัวอย่างการนำหลักคณิตศาสตร์ง่ายๆ มาใช้ในการทำความเข้าใจกับปรัชญาทางโหราศาสตร์ โดยเฉพาะในเรื่องของทฤษฎีพระเคราะห์สนธิ ซึ่งน่าจะทำให้เราเข้าใจมากขึ้น หวังว่าจะเป็นประโยชน์หรือช่วยให้ได้ Idea ในการค้นคว้าศาสตร์แห่งการพยากรณ์ได้ต่อไปไม่มากก็น้อย

ระบบเรือนชะตา ในโหราศาสตร์ยูเรเนียน	การพยากรณ์จร ด้วยโค้งจันทรยาตร์
คณิตคิดสนุก ในทฤษฎีพระเคราะห์สนธิ ตอน 3	คณิตคิดสนุก ในทฤษฎีพระเคราะห์สนธิ ตอน 2
คณิตคิดสนุก ในทฤษฎีพระเคราะห์สนธิ ตอน 1	ความหมายดาวและปัจจัยต่างๆ